ALGORITHMIE
Tout ce qui te faut pour devenir le meilleur en algorithmie !
Tout ce qui te faut pour devenir le meilleur en algorithmie !
SYNTAXE |
OPERATION |
a + b |
Addition |
a - b |
Soustraction |
a * b |
Multiplication |
a / b |
Division (quotient) |
a ** b |
Puissance (a puissance b) |
sqrt(a) |
Racine carré |
a // b |
Quotient de la division euclidienne |
a % b |
Reste de la division euclidienne |
SYNTAXE |
ROLE |
a = 22 |
Affectation des variables |
b = 5.2 |
Affectation des variables |
a,b = 22,5.2 |
Affectation des variables |
a, b = b, a |
Echange les valeurs des variables a et b |
a = a - 1 a -= 1 |
Diminue la variable a de 1 |
a = a + 1 a += 1 |
Incrémente la variable a de 1 |
a = a * 3 a *= 3 |
Multiplication (a multiplié par 3) |
a = a / 2 a /= 2 |
Division réelle |
a = a // 5 a //= 5 |
Division entière |
a = a % 4 a %= 4 |
Reste de la division euclidienne (modulo 4) |
a = a ** 8 a **= 8 |
Puissance |
abs(x) |
Valeur absolue |
int(x) |
Partie entière de l'écriture décimale |
x.conjugate() |
Retourne le conjugué du nombre complexe x |
x.real |
Partie réelle |
x.imag |
Partie imaginaire |
type(a) |
Affiche le type (la classe) de la variable ou de l’objet |
id(a) |
Affiche l’identifiant (l’adresse en mémoire) |
int(x) |
Utilisé pour demander un nombre entier |
float(x) |
Utilisé pour demander un nombre réel |
from math import * eval(x) |
Permet d'entrer une valeur réelle sous la forme d'une racine carré ou d'une fraction |
str(x) |
Utilisé pour demander une chaine de caractère |
complex(a) |
Nombres complexes |
bool |
Booléens (True / False) |
list |
Listes |
set |
Ensembles |
tuple |
n-uplets |
function() |
Fonctions |
|
x & y x and y |
et |
x | y x or y |
ou |
|
x ^ y |
ou exclusif |
not x |
négation de x |
x == y |
Teste si x est égal à y (double égalité) |
x != y |
Teste si x est différent de y |
x < y |
Teste si x est inférieur à y |
x <= y |
Teste si x est inférieur ou égale à y |
x > y |
Teste si x est supérieur à y |
x >= y |
Teste si x est supérieur ou égale à y |
x in y |
Teste si appartenance (pour les listes, ensembles, chaines de caractères) |
x is y |
Teste si identité (comparaison des identifiants de x et y) |
range(a,b,p) |
Retourne les entiers de a à b-1, avec un pas de p |
range(a,b) |
Retourne les entiers de a à b-1, avec la valeur par défaut p=1 |
range(b) |
Retourne les entiers de a à b-1, avec la valeur par défaut a=0 |
randint(a,b) |
Renvoie un entier au hasard entre les entiers a et b inclus |
random() |
Renvoie un nombre au hasard dans l'intervalle [0;1[ |
uniform(a,b) |
Renvoie un nombre au hasard dans l'intervalle [a;b] |
choice(L) |
Renvoie aléatoirement un élément de la liste, ou de la chaine de caractères, L |
|
Importe le module 'math'. On peut ensuite utiliser les fonctions ou les constances sous la forme math.sqrt() ou math.pi ... import math |
Importe les fonctions sin et cos du module 'math'. On peut ensuite les utiliser directement sous la forme sin() ou cos(). from math import sin, cos |
|
Importe le module 'numpy' en le renommant np. On peut ensuite utiliser les fonctions ou le constantes sous la forme np.linspace()... import numpy as np |
L = [] |
Création d'une liste vide |
[1, 2, 3, 4] |
Enumération des objets entre [ ] |
[[1,2], [1], 1] |
Liste dont les deux premiers termes sont des listes |
len(L) |
Longueur (nombre d'éléments) de L |
L1 + L2 |
Concaténation des listes |
n * L |
Pour n entier, concaténation répétée de L avec elle-même |
L.append(a) |
Ajout de l'objet a en fin de la liste |
L.insert(i,a) |
Insertion de l’objet a en position i dans la liste |
L.remove(a) |
Retrait de la première occurrence de a |
L.pop(i) |
Retrait et renvoi de l’élément d’indice i |
L[0] |
Premier élément de la liste |
L[-1] |
Dernier élément de la liste |
del(L[i]) |
Suppression de l'attribut d'indice i |
L.index(a) |
Position de la première occurrence de a |
L.count(a) |
Nombre d'occurrence de a dans la liste |
a in L |
Teste l'appartenance de a à L |
L.copy() |
Copie simple de L |
L.reverse() |
Retourne la liste |
L.sort() |
Trie la liste dans l'ordre croissant |
L.sort() |
Tri simple |
L.sort(reverse=True) |
Tri inversé |
L.sort(key = f) |
Tri suivant la clé donnée par la fonction f |
float(x) |
Utilisé pour demander un nombre réel |
from math import * eval(x) |
Permet d'entrer une valeur réelle sous la forme d'une racine carré ou d'une fraction |
str(x) |
Utilisé pour demander une chaine de caractère |
complex(a) |
Nombres complexes |
bool |
Booléens (True / False) |
list |
Listes |
set |
Ensembles |
tuple |
$n$-uplets |
function() |
Fonctions |
set() |
Ensemble vide |
{1, 2, 3, 4} |
Enumération des objets entre { } |
len(S) |
Cardinal |
S.add(a) |
Ajoute a à l'ensemble S, si pas déjà présent |
S.discard(a) |
Enlève a de S, si c'en est un élément |
S.remove(a) |
Comme discard, mais retourne une erreur si a n'est pas élément de S |
S.pop() |
Retourne et enlève un élément au hasard dans S |
S.intersection(T) |
Retourne l'intersection de S et T |
S.union(T) |
Retourne l'union de S et T |
S.difference(T) |
Retourne les éléments de S qui ne sont pas dans T |
S.isdisjoint(T) |
Retourne True ssi S et T sont disjoints |
S.issubset(T) |
Retourne True ssi S est inclus dans T |
a in S |
Teste l'appartenance de a à S |
S.copy() |
Copie simple de S |
U = () |
Création d'un tuple vide |
(1, 2, 3, 4) |
Enumération des objets entre ( ) |
U[0] |
Premier élément du tuple |
U[-1] |
Dernier élément du tuple |
len(U) |
Longueur (nombre de coordonnées) de U |
U + V |
Retourne la concaténation |
n * U |
Concaténation répétée n fois |
U * n |
Concaténation répétée n fois |
U.count(a) |
Retourne le nombre d'occurrence de a |
U.index(a) |
Retourne le premier indice de a, ou une erreur si a n'est pas un attribut |
a in U |
Teste l'appartenance de a à U |
d = {} |
Création d'un dictionnaire vide |
d = {key1:val1, key2:val2} |
Création d'un dictionnaire à 2 entrée accessibles par les indices key1 et key2 |
d[key1] |
Accès à val1, associé à l'indice key1 |
del(d[key2]) |
Suppression de l'entrée associée à l'indice key2 |
d.keys() |
Donne la liste des clés sous forme d’un itérable |
d.values() |
Donne la liste des valeurs sous forme d’un itérable |
d.items() |
Donne la liste des objets (entrées) sous forme d’un itérable. Les éléments de cet itérable sont des couples (key,val). |
d.pop(key) |
Ressort l’objet associé à la clé key et supprime l'entrée correspondante dans le dictionnaire |
d.popitem() |
Ressort un couple (key,val) du dictionnaire et le supprime |
d.clear() |
Efface tout le contenu du dictionnaire |
|
d = {} d['a'] = (2,3,4) d[5] = 'cinq' d['un'] = 1 |
Création d'un dictionnaire par ajouts successifs |
>>> d |
Affichage du dictionnaire |
>>> d[5] |
Affichage d'une valeur du dictionnaire, associée à une certaine clé |
>>> d[2] |
Accès à une clé non définie |
>>> d['a'] = 23 |
Modification de la valeur associée à une clé |
>>> del d['un'] |
Suppression d'un élément |
'abcd' |
Enumération des caractères successifs entre ' ' |
"abcd" |
Enumération des caractères successifs entre " " |
"""abcd""" |
Enumération des caractères successifs entre """ """ (raw string) |
ch = 'abcd' |
Création d'une chaine de caractères |
>>> ch[2] |
Retourne le 2ème élément de la chaine, ici 'c' |
>>> ch[-1] |
Retourne le dernier élément de la chaine, ici 'd' |
ch = 'azertyuiopqs' |
Création d'une chaine de caractères |
>>> ch[3:8] |
Retourne du 3ème au 8ème élément, ici 'rtyuio' |
>>> ch[::2] |
Retourne 1 élément sur 2, ici 'aetuoq' |
len(c) |
Longueur (nombre de caractères) |
print(c) |
Affichage à l'écran de la chaine c |
c + d |
Concaténation des chaines |
n * c |
Concaténation répétée n fois |
c.join(li) |
Concaténation des chaines de la liste li |
c.split(sep) |
Scinde c en une liste de chaines |
c.center(n) |
Centre n dans une chaine de longueur n |
c.format(x,y,...) |
Insertion des nombres x, y... aux endroits délimités par des { } dans une chaine |
d in c |
Teste si d est sous-chaine de c |
c.count(d) |
Nombre d’occurrences ne se recouvrant pas de la chaîne |
c.find(d) |
Indice de la première occurrence de d (renvoie -1 si pas d'occurrence) |
c.index(d) |
Indice de la première occurrence de d (erreur si pas d'occurrence) |
c.rfind(d) |
De même que find pour la dernière occurrence |
c.rindex(d) |
De même que index pour la dernière occurrence |
c.replace(d,e) |
Remplace toutes les sous-chaînes d par e |
float(a) |
Convertit l’entier a en réel flottant |
complex(a) |
Convertit l’entier ou le flottant a en complexe |
str(x) |
Convertit l’objet x de type quelconque en une chaine de caractères |
list(x) |
Convertit un itérable x (set, tuple, str, range) en objet de type liste |
set(x) |
Convertit un itérable x en set |
tuple(x) |
Convertit un itérable x en tuple |
eval(x) |
Convertit la chaîne x en un objet adéquat, si possible |
float(x) |
Convertit la chaîne x en flottant si possible |
int(x) |
Convertit la chaîne x en entier si possible |
|
Importance des indentations x = y = 1 for i in range(5) x += 1 y += 1 print(x,y) |
Saisie de texte : >>> x = input('Que voulez-vous me dire? ') Que voulez-vous me dire? ZUT! >>> x 'ZUT!' |
|
Saisie de valeur : >>> x = input('Entrez une valeur : ') Entrez une valeur : 2 >>> x '2' |
Saisie de valeur : >>> x = eval(input('Entrez une valeur : ')) Entrez une valeur : 2 >>> x 2 |
|
Syntaxe générale d'une fonction : def nom_de_la_fonction(x,y) : """Description""" instructions return résultat Pour exécuter une fonction, il suffit de l'appeller dans le shell ou dans le code de la manière suivante : nom_de_la_fonction(5,6) |
Exemple de fonction def addition(x,y) : """Action : Fait une addition / Return : Le résultat de l'addition""" a = x + y return a addition(5,6) 11 |
|
Une seule structure à connaitre: if condition1 : instruction(s)1 elif condition2 : instruction(s)2 elif condition3 : instruction(s)3 ... else : instruction(s)4 |
Les clauses elif (il peut y en avoir autant qu’on veut), ainsi que else sont facultatives. La structure est à comprendre comme suit : • Les intructions1 sont effectuées uniquement si le condition1 est positif • Les instructions instructions2 sont effectuées uniquement si le condition1 est négatif et le condition2 positif • Les instructions instructions3 sont effectuées uniquement si le condition1 et le condition2 sont négalifs et le condition3 est positif • ... • Les instructions instructions4 sont effectuées dans tous les autres cas. ATTENTION : N'oubliez pas les deux-points, et faites attention à l'indentation |
|
Une seule structure à connaitre: try : instructions1 except : instructions2 else : instructions3 |
L’ordinateur essaie d’effectuer la série d’instructions1. • S’il survient une erreur d’exécution, il effectue les instructions2 et saute les instructions3. • Sinon, il saute les instructions2 et exécute les instructions3. La clause except est obligatoire, la clause else est facultative. Si on n’a rien a faire dans la clause except, on peut utiliser l’instruction vide pass. |
Import simple du moduleimport mod Cette instruction permet de faire savoir à l'ordinateur qu'on utilise le module 'mod'. On peut alors utiliser les fonctions de ce module en les faisant précéder du préfixe 'mod' (nom du module). mod.fonct() |
Import simple du moduleOn peut, au moment de l’import du module, créer un alias, qui permettra d’appeler les fonctions de ce module en donnant comme préfixe l’alias au lieu du nom complet : import mod as al al.fonct() Un alias d'usage très courant est : import numpy as np |
Import d'une fonction d'un modulefrom mod import fonct Cette instruction permet d'importer la définition de la fonction 'fonct', qui peut alors être utilisée sans préfixe : fonct() |
Import de toutes les fonctions d'un modulefrom mod import * Cette instruction permet d'importer la définition de toutes les fonction du module. |
e |
Constante e, base de l'exponentielle |
exp(x) |
Exponentielle de x |
log(x) |
Logarithme népérien |
log10(x) |
Logarithme en base 10 |
pi |
Le nombre pi |
cos(x) |
Cosinux |
sin(x) |
Sinus |
tan(x) |
Tangente |
acos(x) |
Arscos |
asin(x) |
Arcsin |
atan(x) |
Arctan |
cosh(x) |
Cosinus hyperbolique |
sinh(x) |
Sinus hyperbolique |
tanh(x) |
Tangente hyperbolique |
floor(x) |
Partie entière |
ceil(x) |
Partie entière par excès |
sqrt(x) |
Racine carrée |
factorial(x) |
Factorielle (pour x entier) |
array(liste) |
Convertisseur : Transforme une liste en tableau en imbriquant des listes dans des listes, on peut obtenir des tableaux multidimentionnels |
np.array([1,2,3]) |
Tableau à 3 entrées (matrice ligne) |
np.array([[1,2],[3,4]]) |
Matrice 2x2 de première ligne (1,2) et seconde ligne (3,4) |
np.array([[1],[2][3]]) |
Matrice colonne |
np.shape(A) |
Format du tableau (nb lignes, nb colonnes ...) sous forme d'un tuple |
np.rank(A) |
Profondeur d'imbrication (dimension spatiale) |
np.ones(n) |
Crée une matrice ligne de taille n constituée de 1 |
np.ones((n1,n2)) |
Matrice de taille n1 x n2, constituée de 1 (se généralise à des tuples) |
np.zeros(n) |
Crée une matrice ligne de taille n constituée de 0 |
np.zeros((n1,n2)) |
Matrice de taille n1 x n2, constituée de 0 (se généralise à des tuples) |
np.eye(n) |
Matrice identité d’ordre n (des 1 sur la diagonale) |
np.diag(d0,...,dn) |
Matrice diagonale de coefficients diagonaux d1,...,d_n |
np.linspace(a,b,n) |
Matrice ligne constituée de n valeurs régulièrement réparties (entre $a$ et $b$) |
np.arange(a,b,p) |
Matrice ligne des valeurs de a à b en progressant de pas p |
np.fromfunction(f,(n,)) |
Matrice ligne remplie des valeurs f(k) pour k de 0 à n-1 |
A + B |
Somme de deux matrices |
a * M |
Multiplication par un scalaire |
A * B |
Produit coefficient par coefficient (produit de Schur) |
|
np.dot(A,B) A.dot(B) |
Produit matriciel |
np.linalg.det(A) |
Déterminant |
np.trace(A) |
Trace |
np.transpose(A) |
Transposée |
np.power(A,n) |
A puisssance n |
np.linalg.inv(A) |
Inverse de A |
np.linalg.eigvals(A) |
Valeurs propres de A |
np.linalg.eig(A) |
Valeurs propres et base de valeurs propres |
np.linalg.solve(A,b) |
Donne l’unique solution du système de Cramer Ax=b |
npr.randint(a) |
Génère aléatoirement un entier de 0 à a-1 inclus, de façon uniforme |
npr.randint(a,b) |
Génère aléatoirement un entier de a à b-1 inclus, de façon uniforme |
npr.random(a,b,n) |
Génère un tableau 1 x n d’entiers aléatoirement choisis uniformément entre a et b-1 |
npr.random() |
Génère aléatoirement un réel de [0,1[ de façon uniforme |
npr.sample(n) |
Génère un np.array 1 ligne n colonnes rempli aléatoirement par des réels de [0,1[ choisis uniformément |
npr.sample(tuple) |
De même pour un tableau multidimentionnel de taille définie par le tuple |
|
Intégrale de f de a à b scipy.integrate.quad(f,a,b) |
Résolution d’équation par la méthode de Newton (initailisée au point a, g doit être égal à f') scipy.optimize.newton(f,a,g) |
|
De même par la méthode de la sécante scipy.optimize.newton(f,a) |
Résolution de l’ED y’=f(y,t) (y0 est la valeur initial (t minimal), T est un tableau des temps auquels, calculer les valeurs de y) scipy.integrate.odeint(f,y0,T) |
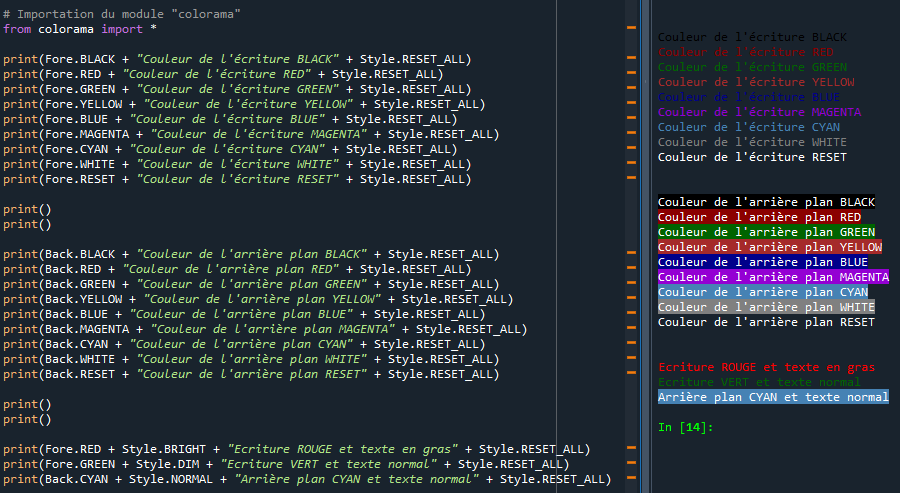
• Fore : permet de changer la couleur de l'écriture,
• Back : permet de changer la couleur de l'arrière plan,
• Style : permet de changer la brillance de la police,
• Style.RESET_ALL : permet de repasser en couleur d'origine.
• Fore : BLACK, RED, GREEN, YELLOW, BLUE, MAGENTA, CYAN, WHITE, RESET
• Back : BLACK, RED, GREEN, YELLOW, BLUE, MAGENTA, CYAN, WHITE, RESET
• Style : DIM, NORMAL, BRIGHT, RESET_ALL
|
Supprimer les tracés précédents plt.clf() |
Tracer la courbe représentant y en fonction de x avec le style styleDuGraphe, l’épaisseur linewidth, le nom de la courbe à afficher dans la légende étant label plt.plot(x, y, styleDuGraphe, linewidth=1, label = 'y = f(x)’) |
|
Ajouter des libellés sur les axes plt.xlabel('x - axe des abscisses') plt.ylabel('y - axe des ordonnées') |
Définir des valeurs minimales et maximales pour les abscisses (-5.5 et 5.5) et les ordonnées (0 et 10) plt.axis([-5.5,5.5,0,10]) ou plt.xlim(-5.5,5.5) plt.ylim(0,10) |
|
Ajouter un titre au graphique plt.title('Représentation de y en fonction de x') |
NB : en ajoutant un r devant la chaîne de caractères, on peut afficher des formules mathématiques à l’aide de la syntaxe LATEX plt.title(r"$\Delta E = \frac{h \times c} {\lambda}$ (J)") |
|
Ajouter une grille au graphique plt.grid() |
|
|
Ajouter du texte dans le graphe à la position souhaitée plt.text(2, 3.5, 'Point de fonctionnement') |
Ajouter une annotation à la position souhaitée xytext et trace une flèche jusqu’au point xy plt.annotate('Maximum', xy=(1.5, 1), xytext=(2,1.5), arrowprops=dict(facecolor='black', arrowstyle='->')) |
|
Tracer un vecteur au point d’application (xVecteur, yVecteur), vecteurX composante suivant x, vecteurY composante suivant y vecteur = plt.quiver(xVecteur, yVecteur, vecteurX, vecteurY, scale=echelleVecteur, color='r',angles='xy', units='xy') |
Trace l’échelle correspondant au vecteur vecteur, en position (0.1,0.1) sur le graphique et valeur de l’échelle. plt.quiverkey(vecteur, 0.1, 0.1, 2, label='échelle 2 m/s', coordinates='data') |
|
Ajouter une légende avec le nom des courbes plt.legend() |
Afficher le graphe plt.show() |
plt.plot(x, y, styleDuGraphe) où styleDuGraphe est une chaîne de caractères qui regroupe la couleur de la courbe, le marqueur de point et le style de liaison entre les points.
CHAINE |
MARQUEUR DE POINT |
. |
Point |
, |
Pixel |
○ |
Rond (alt+9) |
v |
Triangle pointe en bas |
^ |
Triangle pointe en haut |
< |
Triangle pointe à gauche |
> |
Triangle pointe à droite |
1 |
Croix à 3 brancges vers le bas |
2 |
Croix à 3 brancges vers le haut |
3 |
Croix à 3 brancges vers la gauche |
4 |
Croix à 3 brancges vers la droite |
s |
Carré |
p |
Pentagone |
* |
Etoile |
h ou H |
Hexagone |
+ |
Plus |
P |
Plus plein |
x |
Coix |
X |
Croix pleine |
d |
Carreau |
D |
Carreau plus grand |
| |
Barre verticale (altgr+6) |
_ |
Barre horizontale |
CHAINE |
COULEUR ANGLAIS / FRANCAIS |
b |
Blue / Bleu |
g |
Green / Vert |
r |
Red / Rouge |
c |
Cyan / Cyan |
m |
Magenta / Magenta |
y |
Yellow / Jaune |
k |
Black / Noir |
w |
White / Blanc |
CHAINE |
STYLE DE LIGNE |
- |
Ligne continue |
-- |
Tirets |
: |
Ligne en pointillé |
-. |
Tirets points |
plt.plot(x, y, 'r+:') -> Trace un graphe dont les points sont rouges, en forme de + et reliés par des lignes en pointillé.
plt.plot() |
Pour tracer des courbes |
plt.scatter() |
Pour tracer des points |
plt.bar() |
Pour des diagrammes à barre |
plt.bie() |
Pour des camemberts |
plt.hist() |
Pour les histogrammes |
|
Exemple d'utilisation : #classe de niveau 1 classe A(object) : x = 1 def f() : return A.x+1 #class de niveau 2 class B(A) : y = 2 def g() : return B.x+B.y #notion pointée A.x, A.f() # --> 1, 2 B.x, B.f() # --> 1, 2 B.y, B.g() # --> 2, 3 |
Ckasse : class ⚡ Chaque classe définit un espace de noms qui va regrouper attributs (= constantes & variables) et méthodes (=fonctions). ⚡ L'ensemble des attributs associé à une classe est appelé états (state). ⚡ L'ensemble des méthodes associés à une classe est appelé comportement (behavior). |
|
Ckasse : class ⚡ La définition de la classe permet d'associer un identificateur avec un nouveau type de données. ⚡ Synthaxe à utiliser : class child(parent...) : block ⚡ L'ensemble des méthodes associés à une classe est appelé comportement (behavior). |
Exemple d'utilisation : #classe de niveau 1 classe A(object) : x = 1 def f() : return A.x+1 #class de niveau 2 class B(A) : y = 2 def g() : return B.x+B.y #notion pointée A.x, A.f() # --> 1, 2 B.x, B.f() # --> 1, 2 B.y, B.g() # --> 2, 3 |
|
Méthodes spéciales : __init__ : initialisation __repr__ : représentation __str__ : conversion en str __len__ : taille __contains__ : inclusion __eq__ : test == (égal) __le__ test <= (inférieur ou égal) __lt__ : test < (moins de) __add__ : opérateur + __sub__ : opérateur - __call : opérateur () __getitem__ : opérateur [] ... et pleins d'autres ! |
Ckasse : class ⚡ Il existe de nombreux comportements standars pour une classe, qui sont activés simplement en définissant des méthodes dites spéciales avec un prototype prédéfini. ⚡ Ces méthodes spéciales se différencient par leur identificateur spécifique : __name__ |
|
Ckasse : class ⚡ Les méthodes spéciales représentent la base du fonctionnement de Pyton. ⚡ La quasi totalité des instructions mettent en oeuvre un mécanisme de traduction automatique de code par l'interpréteur. ⚡ Ce fonctionnement sera mise en oeuvre pour toutes les classes créées par les développeurs. |
Code utilisateur : A = 1 B = A+1 C = str(A/B) Code interpréteur : int.__init__(A, 1) int.__init__(B, int.__add__(A, 1)) str.__init__(C, float.__str__( int.__div__(A, B))) |
|
Exemple d'utilisation : class A(object) : x = 1 def __init__(self, y): self.y = y # instanciation a = A(0) ; b = A(1) # lecture des attributs a.x, a.y # --> 1, 0 b.x, b.y # --> 1, 1 # édition d'un attribut a.y = 2 # d'instance a.y, b.y # --> 2, 1 # édition d'un attribut A.x = 3 # de classe a.x, b.x # --> 3, 3 |
name = class(...) ⚡ Un attribut défini au niveaude la classe, est commun à toutes les instances, et est appelé attribut de classe (son nom est alors préfixé par le nom de la classe). ⚡ Un attribut défini au niveau d'une instance, est appelé attribut d'instance et n'est pas partagé par les autres instances de la classe (son nom est alorés préfixé par le nom de l'instance). |
|
name = class(...) ⚡ La définition d'une instance (instanciation) permet d'associer un identificateur avec une nouvelle valeur. ⚡ Comme pour les classes, les instances vont définir un espace de noms qui pourra soit contenir des attr ou des méthodes. ⚡ L'accès à cet espace de noms se fera en utilisant la notation pointée. |
Exemple d'utilisation : class A(object) : x = 1 def __init__(self, y): self.y = y # instanciation a = A(0) ; b = A(1) # lecture des attributs a.x, a.y # --> 1, 0 b.x, b.y # --> 1, 1 # édition d'un attribut a.y = 2 # d'instance a.y, b.y # --> 2, 1 # édition d'un attribut A.x = 3 # de classe a.x, b.x # --> 3, 3 |
|
Exemple d'utilisation : class A(object) : x = 1 def __init__(self, y): self.y = y def f() : return -A.x def g(self, x): return self.y + x # instanciation et accès a = A(2) a.x, a.y # --> 1, 2 A.f() # --> -1 a.f() # --> Error a.g(1) # --> 3 A.g(1) # --> Error |
name = class(...) ⚡ Toutes les méthodes sont communes à toutes les instances d'une classe. ⚡ Ce qui différencie une méthode de classe d'une méthode d'instance, est le fait que ces dernières ont systématiquement un 1er paramètre appelé self. ⚡ Dans le bloc d'instructions d'une classe, self correspond à une référence sur l'instance en cours. |
La fonction récurisive est une fonction qui s'appelle elle-même jusqu'à ce qu'elle ne le fasse plus.
La fonction recurs() suivante est une fonction récursive car elle a un appel à elle-même :
def recurs() :
# ...
recurs()
# ...
Pour pouvoir s'arrêter, une fonction récursive doit avoir une condition d'arrêt. Nous devons donc ajouter une instruction if comme celle-ci :
def recurs() :
# ...
if condition :
# ne s'appelle pas elle-même
else :
recurs()
# ...
En règle générale, on utilise une fonction récurisve pour diviser un problème difficiel à résoudre en problèmes plus petis qui sont plus facile à résoudre.
En programmation, vous trouverez souvent les fonctions récursives utilisées dans les structres de données et les algorithmies comme les arbres, les graphiques et les recherches binaires.
Ben, c'est bien, c'est un langage de Programmation !
Attention au Canard !